Skip to main content
Logo image

Basic Analysis I & II: Introduction to Real Analysis, Volumes I & II

Jiří Lebl

Section 10.1 Riemann integral over rectangles

Note: 2–3 lectures
As in Chapter 5, we define the Riemann integral using the Darboux upper and lower integrals. The ideas in this section are very similar to integration in one dimension. The complication is mostly notational. The differences between one and several dimensions will grow more pronounced in the sections following.

Subsection 10.1.1 Rectangles and partitions

Definition 10.1.1.

Let \((a_1,a_2,\ldots,a_n)\) and \((b_1,b_2,\ldots,b_n)\) be such that \(a_k \leq b_k\) for all \(k\text{.}\) The set \([a_1,b_1] \times [a_2,b_2] \times \cdots \times [a_n,b_n]\) is called a closed rectangle. In this setting it is sometimes useful to allow \(a_k = b_k\text{,}\) in which case we think of \([a_k,b_k] = \{ a_k \}\) as usual. If \(a_k < b_k\) for all \(k\text{,}\) then the set \((a_1,b_1) \times (a_2,b_2) \times \cdots \times (a_n,b_n)\) is called an open rectangle.
For an open or closed rectangle \(R \coloneqq [a_1,b_1] \times [a_2,b_2] \times \cdots \times [a_n,b_n] \subset \R^n\) or \(R \coloneqq (a_1,b_1) \times (a_2,b_2) \times \cdots \times (a_n,b_n) \subset \R^n\text{,}\) we define the \(n\)-dimensional volume by
\begin{equation*} V(R) \coloneqq (b_1-a_1) (b_2-a_2) \cdots (b_n-a_n) . \end{equation*}
A partition \(P\) of the closed rectangle \(R = [a_1,b_1] \times [a_2,b_2] \times \cdots \times [a_n,b_n]\) is given by partitions \(P_1,P_2,\ldots,P_n\) of the intervals \([a_1,b_1], [a_2,b_2],\ldots, [a_n,b_n]\text{.}\) We write \(P=(P_1,P_2,\ldots,P_n)\text{.}\) That is, for every \(k=1,2,\ldots,n\) there is an integer \(\ell_k\) and a finite set of numbers \(P_k = \{ x_{k,0},x_{k,1},x_{k,2},\ldots,x_{k,\ell_k} \}\) such that
\begin{equation*} a_k = x_{k,0} < x_{k,1} < x_{k,2} < \cdots < x_{k,{\ell_k}-1} < x_{k,\ell_k} = b_k . \end{equation*}
Picking a set of \(n\) integers \(j_1,j_2,\ldots,j_n\) where \(j_k \in \{ 1,2,\ldots,\ell_k \}\) we get the subrectangle
\begin{equation*} [x_{1,j_1-1}~,~ x_{1,j_1}] \times [x_{2,j_2-1}~,~ x_{2,j_2}] \times \cdots \times [x_{n,j_n-1}~,~ x_{n,j_n}] . \end{equation*}
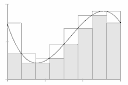
We order the subrectangles somehow and we say \(\{R_1,R_2,\ldots,R_N\}\) are the subrectangles corresponding to the partition \(P\) of \(R\text{,}\) or more simply, subrectangles of \(P\text{.}\) In other words, we subdivided the original rectangle into many smaller subrectangles. See Figure 10.1.
Figure 10.1. Example partition of a rectangle in \(\R^2\text{.}\) The order of the subrectangles is not important.
Let \(R \subset \R^n\) be a closed rectangle and let \(f \colon R \to \R\) be a bounded function. Let \(P\) be a partition of \(R\) with \(N\) subrectangles \(R_1,R_2,\ldots,R_N\text{.}\) Define
\begin{equation*} \begin{aligned} & m_i \coloneqq \inf \bigl\{ f(x) : x \in R_i \bigr\} , & & M_i \coloneqq \sup \bigl\{ f(x) : x \in R_i \bigr\} , \\ & L(P,f) \coloneqq \sum_{i=1}^N m_i V(R_i) , & & U(P,f) \coloneqq \sum_{i=1}^N M_i V(R_i) . \end{aligned} \end{equation*}
We call \(L(P,f)\) the lower Darboux sum and \(U(P,f)\) the upper Darboux sum.
To see the relationship to the \(\Delta\) notation from the one-variable definition, note that when
\begin{equation*} R_i = [x_{1,j_1-1}~,~ x_{1,j_1}] \times [x_{2,j_2-1}~,~ x_{2,j_2}] \times \cdots \times [x_{n,j_n-1}~,~ x_{n,j_n}] , \end{equation*}
then
\begin{equation*} V(R_i) = (x_{1,j_1}-x_{1,j_1-1}) (x_{2,j_2}-x_{2,j_2-1}) \cdots (x_{n,j_n}-x_{n,j_n-1}) = \Delta x_{1,j_1} \Delta x_{2,j_2} \cdots \Delta x_{n,j_n} . \end{equation*}
It is not difficult to see (left to reader) that the subrectangles of \(P\) cover our original \(R\text{,}\) and their volumes sum to that of \(R\text{.}\) That is,
\begin{equation*} R= \bigcup_{k=1}^N R_k , \qquad \text{and} \qquad V(R) = \sum_{k=1}^N V(R_k). \end{equation*}
The indexing in the definition may be complicated, but fortunately we do not need to go back directly to the definition often.

Proof.

Let \(P\) be a partition of \(R\text{.}\) For all \(i\text{,}\) we have \(m \leq m_i \leq M_i \leq M\text{.}\) Also \(\sum_{i=1}^N V(R_i) = V(R)\text{.}\) Therefore,
\begin{multline*} m \, V(R) = m \left( \sum_{i=1}^N V(R_i) \right) = \sum_{i=1}^N m \, V(R_i) \leq \sum_{i=1}^N m_i \, V(R_i) \leq \\ \leq \sum_{i=1}^N M_i \, V(R_i) \leq \sum_{i=1}^N M \,V(R_i) = M \left( \sum_{i=1}^N V(R_i) \right) = M \,V(R) . \qedhere \end{multline*}

Subsection 10.1.2 Upper and lower integrals

By Proposition 10.1.2, the set of upper and lower Darboux sums are bounded sets and we can take their infima and suprema. As in one variable, we make the following definition.

Definition 10.1.3.

Let \(f \colon R \to \R\) be a bounded function on a closed rectangle \(R \subset \R^n\text{.}\) Define
\begin{equation*} \underline{\int_R} f \coloneqq \sup \, \bigl\{ L(P,f) : P \text{ a partition of } R \bigr\} , \qquad \overline{\int_R} f \coloneqq \inf \, \bigl\{ U(P,f) : P \text{ a partition of } R \bigr\} . \end{equation*}
We call \(\underline{\int}\) the lower Darboux integral and \(\overline{\int}\) the upper Darboux integral.
And as in one dimension, we define refinements of partitions.

Definition 10.1.4.

Let \(R \subset \R^n\) be a closed rectangle. Let \(P = ( P_1, P_2, \ldots, P_n )\) and \(\widetilde{P} = ( \widetilde{P}_1, \widetilde{P}_2, \ldots, \widetilde{P}_n )\) be partitions of \(R\text{.}\) We say \(\widetilde{P}\) a refinement of \(P\) if, as sets, \(P_k \subset \widetilde{P}_k\) for all \(k = 1,2,\ldots,n\text{.}\)
If \(\widetilde{P}\) is a refinement of \(P\text{,}\) then subrectangles of \(P\) are unions of subrectangles of \(\widetilde{P}\text{.}\) Simply put, in a refinement, we take the subrectangles of \(P\text{,}\) and we cut them into smaller subrectangles and call that \(\widetilde{P}\text{.}\) See Figure 10.2.
Figure 10.2. Example refinement of the partition from Figure 10.1. New “cuts” are marked in dashed lines. The exact order of the new subrectangles does not matter.

Proof.

We prove the first inequality, and the second follows similarly. Let \(R_1,R_2,\ldots,R_N\) be the subrectangles of \(P\) and \(\widetilde{R}_1,\widetilde{R}_2,\ldots,\widetilde{R}_{\widetilde{N}}\) be the subrectangles of \(\widetilde{R}\text{.}\) Let \(I_k\) be the set of all indices \(j\) such that \(\widetilde{R}_j \subset R_k\text{.}\) For example, in figures 10.1 and 10.2, \(I_4 = \{ 6, 7, 8, 9 \}\) as \(R_4 = \widetilde{R}_6 \cup \widetilde{R}_7 \cup \widetilde{R}_8 \cup \widetilde{R}_9\text{.}\) Then,
\begin{equation*} R_k = \bigcup_{j \in I_k} \widetilde{R}_j, \qquad V(R_k) = \sum_{j \in I_k} V(\widetilde{R}_j). \end{equation*}
Let \(m_j \coloneqq \inf \bigl\{ f(x) : x \in R_j \bigr\}\text{,}\) and \(\widetilde{m}_j \coloneqq \inf \bigl\{ f(x) : \in \widetilde{R}_j \bigr\}\) as usual. If \(j \in I_k\text{,}\) then \(m_k \leq \widetilde{m}_j\text{.}\) Then
\begin{equation*} L(P,f) = \sum_{k=1}^N m_k V(R_k) = \sum_{k=1}^N \sum_{j\in I_k} m_k V(\widetilde{R}_j) \leq \sum_{k=1}^N \sum_{j\in I_k} \widetilde{m}_j V(\widetilde{R}_j) = \sum_{j=1}^{\widetilde{N}} \widetilde{m}_j V(\widetilde{R}_j) = L(\widetilde{P},f) . \qedhere \end{equation*}
The key point of this next proposition is that the lower Darboux integral is less than or equal to the upper Darboux integral.

Proof.

For every partition \(P\text{,}\) via Proposition 10.1.2,
\begin{equation*} m\,V(R) \leq L(P,f) \leq U(P,f) \leq M\,V(R). \end{equation*}
Taking supremum of \(L(P,f)\) and infimum of \(U(P,f)\) over all partitions \(P\text{,}\) we obtain the first and the last inequality in (10.1).
The key inequality in (10.1) is the middle one. Let \(P=(P_1,P_2,\ldots,P_n)\) and \(Q=(Q_1,Q_2,\ldots,Q_n)\) be partitions of \(R\text{.}\) Define \(\widetilde{P} = ( \widetilde{P}_1,\widetilde{P}_2,\ldots,\widetilde{P}_n )\) by letting \(\widetilde{P}_k \coloneqq P_k \cup Q_k\) for every \(k\text{.}\) Then \(\widetilde{P}\) is a partition of \(R\text{,}\) and \(\widetilde{P}\) is a refinement of \(P\) and also a refinement of \(Q\text{.}\) By Proposition 10.1.5, \(L(P,f) \leq L(\widetilde{P},f)\) and \(U(\widetilde{P},f) \leq U(Q,f)\text{.}\) Therefore,
\begin{equation*} L(P,f) \leq L(\widetilde{P},f) \leq U(\widetilde{P},f) \leq U(Q,f) . \end{equation*}
In other words, for two arbitrary partitions \(P\) and \(Q\text{,}\) we have \(L(P,f) \leq U(Q,f)\text{.}\) Via Proposition 1.2.7, we obtain
\begin{equation*} \sup \, \bigl\{ L(P,f) : P \text{ a partition of } R \bigl\} \leq \inf \, \bigl\{ U(P,f) : P \text{ a partition of } R \bigl\} . \end{equation*}
In other words, \(\underline{\int_R} f \leq \overline{\int_R} f\text{.}\)

Subsection 10.1.3 The Riemann integral

We have all we need to define the Riemann integral in \(n\)-dimensions over rectangles. As in one dimension, the Riemann integral is only defined on a certain class of functions, called the Riemann integrable functions.

Definition 10.1.7.

Let \(R \subset \R^n\) be a closed rectangle and \(f \colon R \to \R\) a bounded function such that
\begin{equation*} \underline{\int_R} f(x)\,dx = \overline{\int_R} f(x)\,dx . \end{equation*}
Then \(f\) is said to be Riemann integrable, and we sometimes say simply integrable. We denote the set of Riemann integrable functions on \(R\) by \(\sR(R)\text{.}\) For \(f \in \sR(R)\) define the Riemann integral
\begin{equation*} \int_R f \coloneqq \underline{\int_R} f = \overline{\int_R} f . \end{equation*}
When the variable \(x \in \R^n\) needs to be emphasized, we write
\begin{equation*} \int_R f(x)\,dx, \qquad \int_R f(x_1,\ldots,x_n)\,dx_1 \cdots dx_n, \qquad \text{or} \qquad \int_R f(x)\,dV . \end{equation*}
If \(R \subset \R^2\text{,}\) then we often say area instead of volume, and we write
\begin{equation*} \int_R f(x)\,dA . \end{equation*}
Proposition 10.1.6 immediately implies the following proposition.

Example 10.1.9.

A constant function is Riemann integrable. Proof: Suppose \(f(x) = c\) for all \(x \in R\text{.}\) Then
\begin{equation*} c \, V(R) \leq \underline{\int_R} f \leq \overline{\int_R} f \leq c\, V(R) . \end{equation*}
So \(f\) is integrable, and furthermore \(\int_R f = c\,V(R)\text{.}\)
The proofs of linearity and monotonicity are almost completely identical as the proofs from one variable. We leave the next two propositions as exercises.
Checking for integrability using the definition often involves the following technique, as in the single variable case.

Proof.

First, if \(f\) is integrable, then the supremum of \(L(P,f)\) and infimum of \(U(Q,f)\) over all partitions \(P\) and \(Q\) are equal and hence the infimum of \(U(P,f)-L(Q,f)\) is zero. Taking a common refinement \(\widetilde{P}\) of \(P\) and \(Q\) we find \(U(\widetilde{P},f)-L(\widetilde{P},f) \leq U(P,f)-L(Q,f)\text{.}\) Hence the infimum of \(U(P,f)-L(P,f)\) over all partitions \(P\) is zero, and so for every \(\epsilon > 0\text{,}\) there must be some partition \(P\) such that \(U(P,f) - L(P,f) < \epsilon\text{.}\)
For the other direction, given an \(\epsilon > 0\) find \(P\) such that \(U(P,f) - L(P,f) < \epsilon\text{.}\)
\begin{equation*} \overline{\int_R} f - \underline{\int_R} f \leq U(P,f) - L(P,f) < \epsilon . \end{equation*}
As \(\overline{\int_R} f \geq \underline{\int_R} f\) and the above holds for every \(\epsilon > 0\text{,}\) we conclude \(\overline{\int_R} f = \underline{\int_R} f\) and \(f \in \sR(R)\text{.}\)
Suppose \(f \colon S \to \R\) is a function and \(R \subset S\) is a closed rectangle. If the restriction \(f|_R\) is integrable, then for simplicity we say \(f\) is integrable on \(R\), or \(f \in \sR(R)\text{,}\) and we write
\begin{equation*} \int_R f \coloneqq \int_R f|_R . \end{equation*}

Proof.

Given \(\epsilon > 0\text{,}\) find a partition \(P=(P_1,\ldots,P_n)\) of \(S\) such that \(U(P,f)-L(P,f) < \epsilon\text{.}\) By making a refinement of \(P\) if necessary, assume that the endpoints of \(R\) are in \(P\text{.}\) That is, if \(R = [a_1,b_1] \times [a_2,b_2] \times \cdots \times [a_n,b_n]\text{,}\) then \(a_i,b_i \in P_i\text{.}\) Let \(\widetilde{P} = (\widetilde{P}_1,\ldots,\widetilde{P}_n)\) be the partition of \(R\) given by \(\widetilde{P}_i = P_i \cap [a_i,b_i]\text{.}\) Subrectangles of \(\widetilde{P}\) are subrectangles of \(P\text{,}\) that is, \(R\) is a union of subrectangles of \(P\text{.}\) Divide the subrectangles of \(P\) into two collections: Let \(R_1,R_2\ldots,R_K\) be the subrectangles of \(P\) that are also subrectangles of \(\widetilde{P}\) and let \(R_{K+1},\ldots, R_N\) be the rest. See Figure 10.3. Let \(m_k\) and \(M_k\) be the infimum and supremum of \(f\) on \(R_k\) as usual. Then,
\begin{equation*} \begin{split} \epsilon & > U(P,f)-L(P,f) = \sum_{k=1}^K (M_k-m_k) V(R_k) + \sum_{k=K+1}^N (M_k-m_k) V(R_k) \\ & \geq \sum_{k=1}^K (M_k-m_k) V(R_k) = U(\widetilde{P},f|_R)-L(\widetilde{P},f|_R) . \end{split} \end{equation*}
Therefore, \(f|_R\) is integrable.
Figure 10.3. A partition of a large rectangle \(S\text{,}\) that also gives a partition of a smaller rectangle (shaded and outlined) \(R \subset S\text{.}\) The subrectangles \(R_1,R_2,R_3,R_4\) are the subrectangles of \(\widetilde{P} = \bigl( \{ x_{1,1}, x_{1,2} , x_{1,3} \} , \{ x_{2,1}, x_{2,2} , x_{2,3} \} \bigr)\text{.}\)

Subsection 10.1.4 Integrals of continuous functions

Although we will prove a more general result later, it is useful to start with integrability of continuous functions. To do so, we wish to measure the fineness of partitions. In one variable, we measure the length of a subinterval. In several variables, we measure the sides of a subrectangle. We say a rectangle \(R = [a_1,b_1] \times [a_2,b_2] \times \cdots \times [a_n,b_n]\) has longest side at most \(\alpha\) if \(b_k-a_k \leq \alpha\) for all \(k=1,2,\ldots,n\text{.}\)

Proof.

\begin{equation*} \begin{split} \snorm{x-y} & = \sqrt{ {(x_1-y_1)}^2 + {(x_2-y_2)}^2 + \cdots + {(x_n-y_n)}^2 } \\ & \leq \sqrt{ {(b_1-a_1)}^2 + {(b_2-a_2)}^2 + \cdots + {(b_n-a_n)}^2 } \\ & \leq \sqrt{ {\alpha}^2 + {\alpha}^2 + \cdots + {\alpha}^2 } = \sqrt{n} \, \alpha . \qedhere \end{split} \end{equation*}

Proof.

The proof is analogous to the one-variable proof with some complications. The set \(R\) is a closed and bounded subset of \(\R^n\text{,}\) and hence compact. So \(f\) is uniformly continuous by Theorem 7.5.11. Let \(\epsilon > 0\) be given. Find a \(\delta > 0\) such that \(\snorm{x-y} < \delta\) implies \(\sabs{f(x)-f(y)} < \frac{\epsilon}{V(R)}\text{.}\)
Let \(P\) be a partition of \(R\text{,}\) such that longest side of every subrectangle is strictly less than \(\frac{\delta}{\sqrt{n}}\text{.}\) If \(x, y \in R_k\) for a subrectangle \(R_k\) of \(P\text{,}\) then, by the proposition, \(\snorm{x-y} < \sqrt{n} \frac{\delta}{\sqrt{n}} = \delta\text{.}\) Therefore,
\begin{equation*} f(x)-f(y) \leq \sabs{f(x)-f(y)} < \frac{\epsilon}{V(R)} . \end{equation*}
As \(f\) is continuous on \(R_k\text{,}\) which is compact, \(f\) attains a maximum and a minimum on this subrectangle. Let \(x\) be a point where \(f\) attains the maximum and \(y\) be a point where \(f\) attains the minimum. Then \(f(x) = M_k\) and \(f(y) = m_k\) in the notation from the definition of the integral. Thus,
\begin{equation*} M_k-m_k = f(x)-f(y) < \frac{\epsilon}{V(R)} . \end{equation*}
And so
\begin{equation*} \begin{split} U(P,f) - L(P,f) & = \left( \sum_{k=1}^N M_k V(R_k) \right) - \left( \sum_{k=1}^N m_k V(R_k) \right) \\ & = \sum_{k=1}^N (M_k-m_k) V(R_k) \\ & < \frac{\epsilon}{V(R)} \sum_{k=1}^N V(R_k) = \epsilon. \end{split} \end{equation*}
Via application of Proposition 10.1.12, we find that \(f \in \sR(R)\text{.}\)

Subsection 10.1.5 Integration of functions with compact support

Let \(U \subset \R^n\) be an open set and \(f \colon U \to \R\) be a function. The support of \(f\) is the set
\begin{equation*} \operatorname{supp} (f) \coloneqq \overline{ \{ x \in U : f(x) \not= 0 \} } , \end{equation*}
where the closure is with respect to the subspace topology on \(U\text{.}\) Taking the closure with respect to the subspace topology is the same as \(\overline{ \{ x \in U : f(x) \not= 0 \} } \cap U\text{,}\) where the closure is with respect to the ambient euclidean space \(\R^n\text{.}\) In particular, \(\operatorname{supp} (f) \subset U\text{.}\) The support is the closure (in \(U\)) of the set of points where the function is nonzero. Its complement in \(U\) is open. If \(x \in U\) and \(x\) is not in the support of \(f\text{,}\) then \(f\) is constantly zero in a whole neighborhood of \(x\text{.}\)
A function \(f\) is said to have compact support if \(\supp(f)\) is a compact set.

Example 10.1.16.

The function \(f \colon \R^2 \to \R\) defined by
\begin{equation*} f(x,y) \coloneqq \begin{cases} -x{(x^2+y^2-1)}^2 & \text{if } \sqrt{x^2+y^2} \leq 1, \\ 0 & \text{else}, \end{cases} \end{equation*}
is continuous and its support is the closed unit disc \(C(0,1) = \bigl\{ (x,y) : \sqrt{x^2 + y^2} \leq 1 \bigr\}\text{,}\) which is a compact set, so \(f\) has compact support. Note that the function is zero on the entire \(y\)-axis and on the unit circle, but all points that lie in the closed unit disc are still within the support as they are in the closure of points where \(f\) is nonzero. See Figure 10.4.
Figure 10.4. Function with compact support (left), the support is the closed unit disc (right).
If \(U \not= \R^n\text{,}\) then you must be careful to take the closure in \(U\text{.}\) Consider the following two examples.

Example 10.1.17.

Let \(B(0,1) \subset \R^2\) be the unit disc. The function \(f \colon B(0,1) \to \R\) defined by
\begin{equation*} f(x,y) \coloneqq \begin{cases} 0 & \text{if } \sqrt{x^2+y^2} > \nicefrac{1}{2}, \\ \nicefrac{1}{2} - \sqrt{x^2+y^2} & \text{if } \sqrt{x^2+y^2} \leq \nicefrac{1}{2}, \end{cases} \end{equation*}
is continuous on \(B(0,1)\) and its support is the smaller closed ball \(C(0,\nicefrac{1}{2})\text{.}\) As that is a compact set, \(f\) has compact support.
The function \(g \colon B(0,1) \to \R\) defined by
\begin{equation*} g(x,y) \coloneqq \begin{cases} 0 & \text{if } x \leq 0, \\ x & \text{if } x > 0, \end{cases} \end{equation*}
is continuous on \(B(0,1)\text{,}\) but its support is the set \(\bigl\{ (x,y) \in B(0,1) : x \geq 0 \bigr\}\text{.}\) In particular, \(g\) is not compactly supported.
We really only need to consider the case when \(U=\R^n\text{.}\) In light of Exercise 10.1.1, which says every continuous function on an open \(U \subset \R^n\) with compact support can be extended to a continuous function with compact support on \(\R^n\text{,}\) considering \(U=\R^n\) is not an oversimplification.

Example 10.1.18.

The continuous function \(f \colon B(0,1) \to \R\) given by \(f(x,y) \coloneqq \sin\bigl(\frac{1}{1-x^2-y^2}\bigr)\) does not have compact support; as \(f\) is not constantly zero on any neighborhood of every point in \(B(0,1)\text{,}\) the support is the entire disc \(B(0,1)\text{.}\) The function does not extend as above to a continuous function on \(\R^2\text{.}\) In fact, it is not difficult to show that \(f\) cannot be extended in any way whatsoever to be continuous on all of \(\R^2\) (the boundary of the disc is the problem).

Proof.

As \(f\) is continuous, it is automatically integrable on the rectangles \(R\text{,}\) \(S\text{,}\) and \(R \cap S\text{.}\) Then Exercise 10.1.7 says \(\int_S f = \int_{S \cap R} f = \int_R f\text{.}\)
Because of this proposition, when \(f \colon \R^n \to \R\) has compact support and is integrable on a rectangle \(R\) containing the support, we write
\begin{equation*} \int f \coloneqq \int_R f \qquad \text{or} \qquad \int_{\R^n} f \coloneqq \int_R f . \end{equation*}
For example, if \(f\) is continuous and of compact support, then \(\int_{\R^n} f\) exists.

Exercises 10.1.6 Exercises

10.1.1.

Suppose \(U \subset \R^n\) is open and \(f \colon U \to \R\) is continuous and of compact support. Show that the function \(\widetilde{f} \colon \R^n \to \R\)
\begin{equation*} \widetilde{f}(x) \coloneqq \begin{cases} f(x) & \text{if } x \in U, \\ 0 & \text{otherwise,} \end{cases} \end{equation*}
is continuous.

10.1.3.

Suppose \(R\) is a closed rectangle with the length of one of the sides equal to 0. For every bounded function \(f \colon R \to \R\text{,}\) show that \(f \in \sR(R)\) and \(\int_R f = 0\text{.}\)

10.1.4.

Suppose \(R\) is a closed rectangle with the length of one of the sides equal to 0, and suppose \(S\) is a closed rectangle with \(R \subset S\text{.}\) If \(f \colon S \to \R\) is a bounded function such that \(f(x) = 0\) for \(x \in S \setminus R\text{,}\) show that \(f \in \sR(S)\) and \(\int_S f = 0\text{.}\)

10.1.5.

Suppose \(f\colon \R^n \to \R\) is such that \(f(x) \coloneqq 0\) if \(x\not= 0\) and \(f(0) \coloneqq 1\text{.}\) Show that \(f\) is integrable on \(R \coloneqq [-1,1] \times [-1,1] \times \cdots \times [-1,1]\) directly using the definition, and find \(\int_R f\text{.}\)

10.1.6.

Suppose \(R\) is a closed rectangle and \(h \colon R \to \R\) is a bounded function such that \(h(x) = 0\) if \(x \notin \partial R\) (the boundary of \(R\)). Let \(S\) be a closed rectangle. Show that \(h \in \sR(S)\) and
\begin{equation*} \int_{S} h = 0 . \end{equation*}
Hint: Write \(h\) as a sum of functions as in Exercise 10.1.4.

10.1.7.

Suppose \(R\) and \(R'\) are two closed rectangles with \(R' \subset R\text{.}\) Suppose \(f \colon R \to \R\) is in \(\sR(R')\) and \(f(x) = 0\) for \(x \in R \setminus R'\text{.}\) Show that \(f \in \sR(R)\) and
\begin{equation*} \int_{R'} f = \int_R f . \end{equation*}
Do this in the following steps.
  1. First do the proof assuming that furthermore \(f(x) = 0\) whenever \(x \in \overline{R \setminus R'}\text{.}\)
  2. Write \(f(x) = g(x) + h(x)\) where \(g(x) = 0\) whenever \(x \in \overline{R \setminus R'}\text{,}\) and \(h(x)\) is zero except perhaps on \(\partial R'\text{.}\) Then show \(\int_R h = \int_{R'} h = 0\) (see Exercise 10.1.6).
  3. Show \(\int_{R'} f = \int_R f\text{.}\)

10.1.8.

Suppose \(R' \subset \R^n\) and \(R'' \subset \R^n\) are two rectangles such that \(R = R' \cup R''\) is a rectangle, and \(R' \cap R''\) is rectangle with one of the sides having length 0 (that is \(V(R' \cap R'') = 0\)). Let \(f \colon R \to \R\) be a function such that \(f \in \sR(R')\) and \(f \in \sR(R'')\text{.}\) Show that \(f \in \sR(R)\) and
\begin{equation*} \int_{R} f = \int_{R'} f + \int_{R''} f . \end{equation*}
Hint: See previous exercise.

10.1.9.

Prove a stronger version of Proposition 10.1.19. Suppose \(f \colon \R^n \to \R\) is a function with compact support but not necessarily continuous. Prove that if \(R\) is a closed rectangle such that \(\operatorname{supp}(f) \subset R\) and \(f\) is integrable on \(R\text{,}\) then for every other closed rectangle \(S\) with \(\operatorname{supp}(f) \subset S\text{,}\) the function \(f\) is integrable on \(S\) and \(\int_S f = \int_R f\text{.}\) Hint: See Exercise 10.1.7.

10.1.10.

Suppose \(R\) and \(S\) are closed rectangles of \(\R^n\text{.}\) Define \(f \colon \R^n \to \R\) as \(f(x) \coloneqq 1\) if \(x \in R\text{,}\) and \(f(x) \coloneqq 0\) otherwise. Prove \(f\) is integrable on \(S\) and compute \(\int_S f\text{.}\) Hint: Consider \(S \cap R\text{.}\)

10.1.11.

Let \(R \coloneqq [0,1] \times [0,1] \subset \R^2\text{.}\)
  1. Suppose \(f \colon R \to \R\) is defined by
    \begin{equation*} f(x,y) \coloneqq \begin{cases} 1 & \text{if } x = y, \\ 0 & \text{else.} \end{cases} \end{equation*}
    Show that \(f \in \sR(R)\) and compute \(\int_R f\text{.}\)
  2. Suppose \(f \colon R \to \R\) is defined by
    \begin{equation*} f(x,y) \coloneqq \begin{cases} 1 & \text{if } x \in \Q \text{ or } y \in \Q, \\ 0 & \text{else.} \end{cases} \end{equation*}
    Show that \(f \notin \sR(R)\text{.}\)

10.1.12.

Suppose \(R\) is a closed rectangle, and suppose \(S_j\) are closed rectangles such that \(S_j \subset R\) and \(S_j \subset S_{j+1}\) for all \(j\text{.}\) Suppose \(f \colon R \to \R\) is bounded and \(f \in \sR(S_j)\) for all \(j\text{.}\) Show that \(f \in \sR(R)\) and
\begin{equation*} \lim_{j\to\infty} \int_{S_j} f = \int_R f . \end{equation*}

10.1.13.

Suppose \(f\colon [-1,1] \times [-1,1] \to \R\) is a Riemann integrable function such \(f(x) = -f(-x)\text{.}\) Using the definition prove
\begin{equation*} \int_{[-1,1] \times [-1,1]} f = 0 . \end{equation*}
PrevTopNext
For a higher quality printout use the PDF versions: https://www.jirka.org/ra/realanal.pdf or https://www.jirka.org/ra/realanal2.pdf